Table of Contents
- Gestione previsioni con il metodo Holt Winters
- Holt Winters: metodo statistico per costruire le previsioni
- Holt Winters: esposizione dettagliata
- Calcolo valori al periodo 0
- Holt Winters moltiplicativo
- Azioni tra due viste
- Introduzione
- Operatori PRIOR e PRIORF (Priorità vista)
- Operatori SIV2 e SIV2F (Selezione vista da presenza)
- Operatori NOV2 e NOV2F (Selezione vista da assenza)
- Operatore COLF (Completamento oltre frontiera)
- FUNZIONI NUMERICHE
- Introduzione
- Funzioni implementate
- Funzioni scalari di un numero
- Funzioni vettoriali di un numero
- Funzioni scalari di una serie
- Funzioni vettoriali di una serie
- Funzioni scalari di due serie
- Funzioni vettoriali di due serie
- Utilizzo della /COPY
- Funzione INZ (inizializzazione)
- Funzione CAR (caricamento)
- Funzione Fxx (esecuzione funzione)
- Descrizione formule utilizzate
- F01102 - Valore attuale
- F03300 - Numero Elementi
- F03301 - Somma
- F03302 - Media
- F03303 - Varianza
- F03304 - Deviazione standard
- F03305 - MAD
- F03306 - MSD
- F03307 - CV
- F03360 - Mediana
- F03361 - CP
- F03362 - CPL
- F03363 - CPU
- F03364 - CPK
- F03365 - CPM
- F03366 - CPKM
- F06612 - Accuracy
- Algoritmo del sacco
- Descrizione tecnica.
- Note
- Previsioni con HW
- Previsioni con Holt Winters
- Introduzione
- Impostazioni
- Periodicità
- Frontiera
- Numero periodi di previsione
- Numero periodi di storia
- Numero periodi iniziali
- Esempio di impostazione periodi
- Fattori di smorzamento
- Autofit senza arretramento
- HW Moltiplicativo
- Mantiene negativi
- N. Decimali di arrotondamento
- Indice autofit
- Memorizzazione numeri
- Numeri di dettaglio
- Numeri di riepilogo generali
- Numeri di riepilogo per plant.
- Vista di statistica Hotelling
- Previsioni con Regressione lineare
- Introduzione
- Impostazioni
- Frontiera
- Numero periodi di previsione
- Numero periodi di storia
- Esempio di impostazione periodi
- Mantiene negativi
- N. Decimali di arrotondamento
- Previsioni con scelta metodo
- Previsioni: Correzione serie
- Sostituzione articolo
- Esempi grafici di sostituzione
- Sostituzione articolo 1 -> N
- Sostituzione nel passato
- Sostituzione nel futuro
- Esempio grafici di sostituzione
- Indici Previsioni articolo
- Descrizione Indici Previsioni articolo
- - Documentazione generale del tema
- null01 - MAPE consuntivo
- 02 - SIGMA consuntivo
- 03 - Errore % Consuntivo
- 04 - Numero toccate
- 05 - Classe previsionale
- 06 - Profondità della storia
- 07 - Max alfa,beta,gamma
- 08 - Giorni a lead time
- 09 - Giorni a fine periodo
- 10 - Passo
- 11 - Incertezza a N passi
- 12 - Incertezza proporzionale
- 13 - Data sfondamento
- 14 - N.elementi fuori limite
- 15 - Valore limite
- Classe previsiva articolo
- Scorta minima e calcolo / utilizzo scorta minima dinamica
- Scorta minima
- Introduzione
- Impostazione in dati articolo / plant
- Priorità di scelta
- Modalità di calcolo scorta
- Valori consigliati per la tabella MP2
- Modalità di richiamo - In fonti di disponibilità
- Modalità di richiamo - In routine £M5A
- Fonti esistenti e future
- Popolamento dati articolo/plant
- Analisi azione utente MPAP01_X
Gestione previsioni con il metodo Holt Winters
E' stato realizzato uno strumento avanzato di previsioni (con il metodo di Holt Winters, nel seguito HW), utilizzabile sia in applicazioni personali, sia in apposite funzioni MPS. Holt Winters: metodo statistico per costruire le previsioni
Il metodo Holt Winters (HW) si applica ad una serie storica per ottenere una previsione dei periodi futuri.In fase di messa a punto, per verificarne l'efficacia, esso può essere utilizzato in controllo, vale a dire facendogli fare una previsione per periodi passati, di cui si dispongono già i valori effettivi.
Definiamo:
- Frontiera, l'ultimo periodo della serie che si assume come storia. Le previsioni iniziano dal periodo successivo. La frontiera non coincide con l'ultimo periodo della serie nel caso del controllo e, come vedremo, nell'autofit;
- Periodicità, il numero di periodi in seguito a cui si assume che la serie presenti una ripetitività;
- Storia, il numero di periodi passati su cui si fonda la previsione. Per il metodo HW è necessaria (e sufficiente) una storia pari a due periodicità;
- Numero di periodi di previsione, il numero di periodi futuri (da quello successivo alla frontiera in poi) per cui si calcola la previsione;
- Numero di periodi iniziali, il numero di periodi, a partire dal primo periodo della storia, su cui si esegue un'interpolazione lineare per ottenere i dati di "innesco" del calcolo. Può essere al massimo pari alla periodicità; un valore minore riduce il peso della storia nel calcolo.
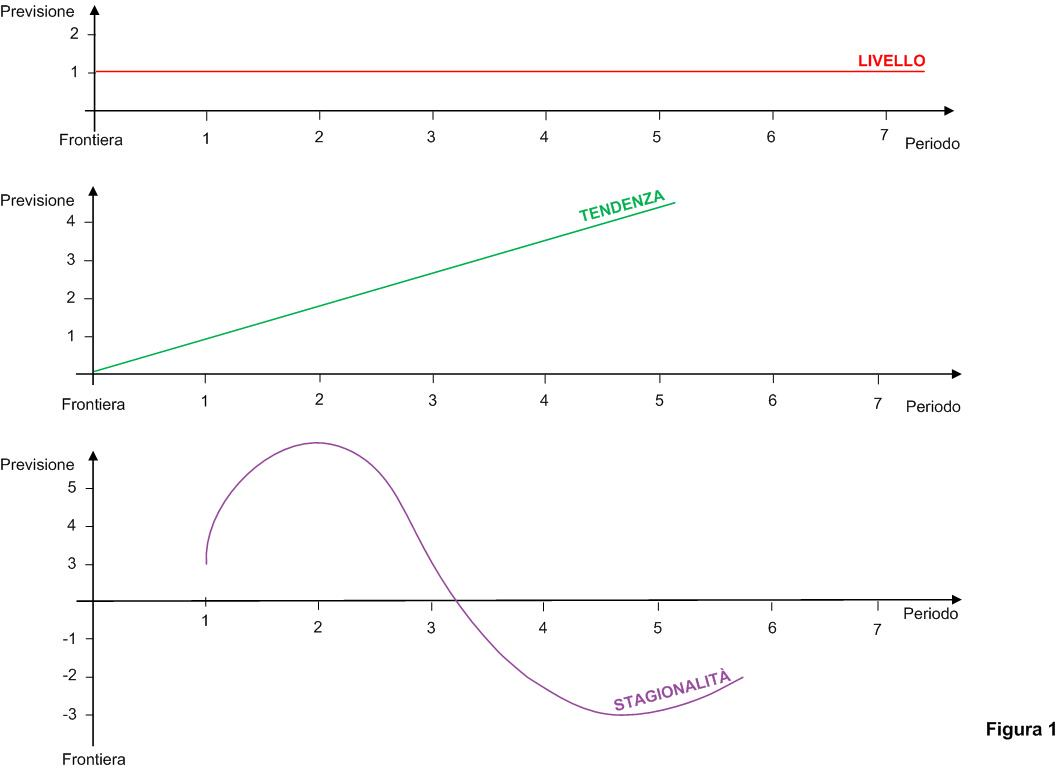
Il metodo HW si basa su tre valori, tutti nella stessa unità di misura della serie, che si determinano alla frontiera:
- Livello --> valore medio della previsione nei periodi futuri;
- Trend --> variazione (che si assume costante) della previsione rispetto al periodo precedente. Se positivo indica una crescita, se negativo una diminuzione;
- Stagionalità --> una serie di "P" valori (dove "P" è la periodicità) che indica, rispetto al livello, la variazione della previsione dovuta a fenomeni ripetitivi).
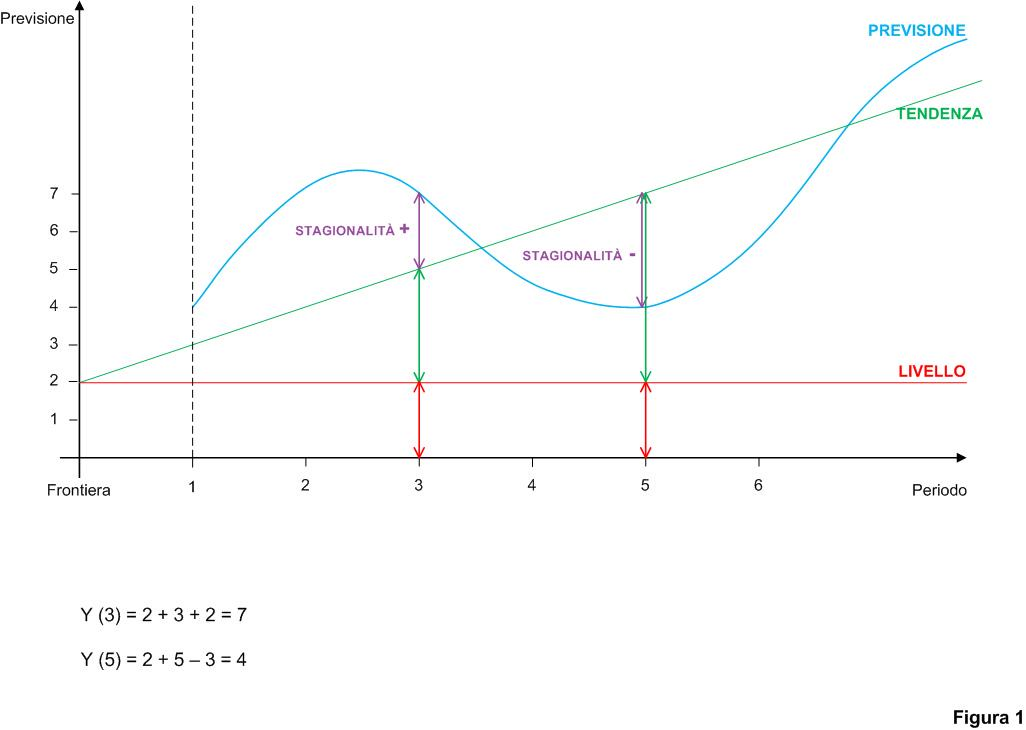
La previsione del periodo "N" (da 1 al numero di periodi di previsione) è data da:
Livello + N x Trend + Stagionalità del periodo N.
La determinazione di livello, trend e stagionalità, richiede che si impostino tre fattori di smorzamento (il cui valore va da 0 a 1) indicanti il peso dei periodi più recenti rispetto a quelli più in là nel tempo. Il valore 0 significa che conta solo il periodo iniziale. Il valore 1 significa che conta solo l'ultimo periodo (frontiera).
Essi sono:
- Alfa per il livello
- Beta per il trend
- Gamma per la stagionalità
Si presenta quindi il problema di come impostarli in modo da massimizzare l'efficacia della previsione.
Dall'esperienza, un valore di 0,2 per tutti e tre pare dia risultati accettabili.
Un modo più evoluto (che richiede però tempi di elaborazione molto più lunghi) è l'autofit, in cui si fanno calcolare al sistema i valori ottimi dei tre fattori di smorzamento.
L'ottimo si definisce come la terna dei valori che minimizza un coefficiente generale di bontà della previsione (CB), che può essere scelto tra
 |
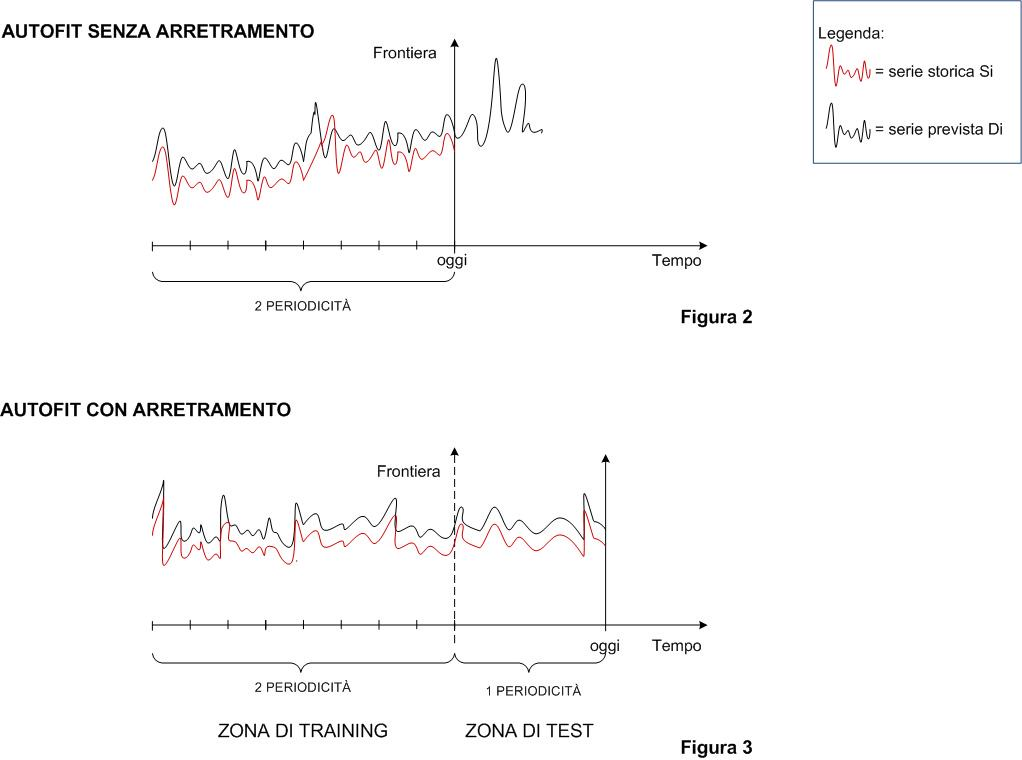
Disponendo di una serie di tre periodicità, la frontiera viene portata alla fine delle prime due (che costituiscono la zona di training). Viene quindi calcolata la previsione per la terza periodicità (zona di test) per tutte le combinazioni di alfa, beta e gamma (con un passo impostato, ad esempio di 0,2), e si determina il CB, confrontando, nella zona di test, la previsione calcolata con i valori storici.
Viene quindi eseguita la previsione, con la frontiera riportata al valore iniziale, con la terna di fattori che ha minimizzato il CB.
Non disponendo di una serie di tre periodicità, ma solo di due (che è la condizione minima per l'applicabilità di HW), si opera nel seguente modo (autofit senza arretramento): durante l'elaborazione, per determinare i coefficienti di livello, trend e stagionalità sulla frontiera, viene calcolata, per ogni periodo della storia, la previsione, partendo dai valori di livello, trend e stagionalità dello stesso periodo; si esegue, come nel caso precedente, l'elaborazione per tutte le combinazioni di alfa, beta e gamma e si determina il CB confrontando la serie storica con la previsione "storica"; la parte successiva del metodo coincide con il caso predecente.
A questo proposito facciamo presente che il sistema comunque calcola sempre i valori dei tre CB consuntivi per la parte storica.
ESEMPI
Riportiamo alcuni esempi di previsioni, con le seguenti assunzioni:
- Il periodo della serie è il mese.
- La periodicità è di 12 periodi.
- La storia è di 24 periodi (12 x 2).
- Il numero di periodi di previsione è 12.
A) Previsione con una serie di 24 periodi
E' la condizione minima per eseguire l'HW.
- Si può impostare solo l'autofit senza arretramento.
- In alternativa si fissano i valori dei tre fattori di smorzamento.
- Vengono calcolate le previsioni per i periodi dal 25 al 36.
B) Previsione con una serie di 36 periodi
- La frontiera è al periodo 36, quindi è possibile eseguire l'autofit "normale", in quanto c'è possibilità di separate i periodi di trainining (i primi 24 mesi) e quelli di test (gli ultimi dodici).
- In alternativa si fissano i valori dei tre fattori di smorzamento, con la frontiera al periodo 36 e una storia di 24 periodi, ottenendo la previsione per i periodi dal 37 al 48.
- In questa situazione, sarebbe possibile utilizzare tutti i 36 periodi di storia (nel calcolo finale, non nell'autofit), ma i risultati non sembrano differire significativamente da quelli ottenuti impostando per la storia il valore normale di 24 periodi.
C) Controllo con una serie di 36 periodi
In questo caso si vuole controllare, dall'esterno, l'attendibilità della previsione.
- Si deve fissare la frontiera al periodo 24, in modo che il sistema preveda i periodi dal 25 al 36, impostando comunque che la serie storica è composta di 36 periodi.
- Ci si riconduce quindi al caso A), e quindi è possibile unicamente l'autofit senza arretramento.
- In più, dato che il sistema riconosce che è stata fornita una serie storica anche nel futuro (periodi dal 25 al 36) calcola i CB previsionali, confrontando questi valori con quelli calcolati per gli stessi periodi.
- Dato che vengono comunque calcolati i CB consuntivi, il sistema è in grado di calcolare anche i CB totali, che utilizzano le due serie nella loro completezza (dal periodo 1 al 36, sia per la per la serie storica che per quella previsionale, composta dai periodi dall'1 al 24 per la previsione nel "passato" e da quelli dal 25 al 36 per la previsione nel "futuro").
D) Controllo con una serie di 48 periodi
Anche in questo caso si vuole controllare, dall'esterno, l'attendibilità della previsione.
- Si deve fissare la frontiera al periodo 36, in modo che il sistema preveda i periodi dal 37 al 48, impostando comunque che la serie storica è composta di 48 periodi, mentre la storia è di 24.
- Ci si riconduce quindi al caso B), pertanto è possibile utilizzare l'autofit "normale".
- Le ulteriori considerazioni (calcolo dei CB previsionali e totali) sono le stesse del caso C).
 |
 |
 |
Holt Winters: esposizione dettagliata
La previsione di un periodo futuro n dipende dai valori di livello, trend e stagionalità, relativi alla frontiera (ultimo periodo della storia), con la seguente formula: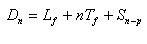 |
 |
Si utilizzano le seguenti formule, che permettono di calcolare il valore per il generico periodo i+1 a partire dal valore del periodo i.
Esse vanno applicate ricorsivamente, a partire dai valori del periodo 1 (inizio della storia) fino a quelli del periodo f (frontiera).
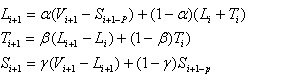 |
 |
Anche i valori del periodo 1 vengono calcolati nello stesso modo, partendo dai valori del periodo precedente (periodo 0), che invece si determinano in modo specifico, partendo dai dati della serie storica.
Calcolo valori al periodo 0
Per il livello e il trend si calcola la retta che interpola la serie storica, a partire dal periodo 1, per una periodicità. Il livello e il trend sono, rispettivamente, l'ordinata all'origine e il coefficiente angolare di questa retta.Per la stagionalità, che è costituita da un vettore con un numero di elementi pari a una periodicità, si opera determinando la retta che interpola la serie storica per tutti i periodi e se ne ricava, per ogni periodo, il residuo (differenza tra il valore della serie e quello della retta interpolatrice).
La stagionalità del periodo n è data dalla media aritmetica dei residui del periodo n , n+p, n+2p, (dove p è la periodicità), fino a che questo indice supera la storia.
Ad esempio, con una storia di 31 periodi e una periodicità di 12, si determina il seguente vettore di stagionalità:
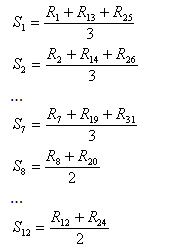 |
 |
Holt Winters moltiplicativo
Il metodo descritto in precedenza è di tipo additivo: le tre componenti si sommano per ottenere la previsione e hanno quindi tutte la stessa unità di misura della previsione.Esiste anche un metodo moltiplicativo in cui, per ottenere la previsione, si sommano il livello e il trend (in modo analogo al metodo additivo) e si moltiplica il risultato per la stagionalità, che in questo caso è un valore adimensionale.
Il metodo moltiplicativo risponde in maniera più nervosa alla stagionalità.
Azioni tra due viste
Introduzione
Partendo da due viste dello stesso oggetto, o della stessa coppia di oggetti, si ottiene una terza vista, a pari chiave, applicando un operatore alle quantità dello stesso periodo. Operatori PRIOR e PRIORF (Priorità vista)
- PRIOR: copia nel risultato la vista 1 se ha almeno un elemento diverso da zero, altrimenti copia la vista 2. Con questo operatore un risultato viene sempre scritto, in quanto non può verificarsi il caso di contemporanea assenza di entrambe le viste.
- PRIORF: copia nel risultato la vista 1 se presente il record, altrimenti copia la vista 2. Con questo operatore un risultato viene sempre scritto, in quanto non può verificarsi il caso di contemporanea assenza di entrambe le viste.
 |
Operatori SIV2 e SIV2F (Selezione vista da presenza)
- S IV2: se la vista 2 ha almeno un campo diverso da zero, copia nel risultato la vista 1, a patto che quest'ultima esista. Con questo operatore non è detto che venga scritta una vista.
- SIV2F: se presente la vista 2, copia nel risultato la vista 1, a patto che quest'ultima esista. Con questo operatore non è detto che venga scritta una vista.
 |
Operatori NOV2 e NOV2F (Selezione vista da assenza)
- NOV2: se la vista 2 esiste e ha tutti i campi uguali a zero, copia nel risultato la vista 1, a patto che quest'ultima esista. Con questo operatore non è detto che venga scritta una vista.
- NOV2F: se assente la vista 2, copia ne risultato la vista 1, a patto che quest'ultima esista. Con questo operatore non è detto che venga scritta una vista.
 |
Operatore COLF (Completamento oltre frontiera)
Operatore che scrive, nella vista del risultato, parte delle quantità della vista 2, in base al riempimento (frontiera) della vista 1. |
FUNZIONI NUMERICHE
Introduzione
Scopo della /COPY G56 è l'esecuzione di operazioni matematiche su numeri, serie e coppie di serie. Una serie è una sequenza di numeri, la si può rappresentare geometricamente come un insieme di punti su una retta su cui è stata definita l'origine. Una coppia di serie è formata da due sequenze di numeri, la si può rappresentare come un insieme di punti nel piano cartesiano, ciascuno con l'ascissa costituita dalla seconda serie e l'ordinata dalla prima; il numero di elementi delle due serie è lo stesso, in quanto costituisce il numero di punti. Un modo particolare di definizione delle due serie è quello in cui la seconda è il "passo unitario" della prima. In tal caso essa viene riempita automaticamente nel seguente modo: se la prima serie è composta da questi 5 elementi: 23, 12, 34, 45, 0; viene riempita la seconda con le posizioni della prima; 1, 2, 3, 4, 5.NB: questo è unicamente un modo di inserire automaticamente la seconda serie, che potrebbe essere inserita manualmente, senza che nulla cambi nei risultati.
E' possibile calcolare:
- funzioni scalari: viene ritornato un numero, o un insieme di numeri di significato diverso. Un esempio del primo caso è la media di una serie. Un esempio del secondo caso è la regressione lineare di due serie, il cui risultato è costituito da due numeri: il coefficiente angolare e l'ordinata all'origine della retta interpolatrice.
- funzioni vettoriali: viene ritornata una serie di numeri con significato omogeneo. E' possibile calcolare funzioni vettoriali anche sui numeri: un esempio è la scomposizione in numeri primi. Nel caso di funzioni vettoriali su serie, la serie di output può avere lo stesso numero di elementi dell'ingresso, o un numero diverso.
Un esempio del secondo caso è la previsione con il metodo Holt Wilters: viene ritornato un numero di elementi pari a quello della serie di input sommato al numero di periodi di previsione.
In taluni casi, le funzioni vettoriali ritornano, come "effetto collaterale", anche degli scalari. Un esempio è ancora la previsione Holt Winters, in cui vengono ritornati gli indici di bontà della previsione stessa.
Funzioni implementate
Funzioni scalari di un numero
Fattoriale (viene calcolato se il numero di input è inferiore a 20, per motivi di overflow)Attualizzazione di un valore: dato un montante (valore finale), la data iniziale e finale, e un valore di interesse, viene ritornato il valore attualizzato, che porta al montante, in caso di interesse composto su base annuale.
Funzioni vettoriali di un numero
Scomposizione in numeri primi (viene calcolato se il numero di input è inferiore a 10000, per motivi implementativi) Funzioni scalari di una serie
Numero elementi (1)Somma
Media
Varianza
Deviazione standard
MAD
MSD
Numero elementi non a zero
Somma elementi non a zero
Media elementi non a zero
Varianza elementi non a zero
Dev. Std elementi non a zero
MAD elementi non a zero
MSD elementi non a zero
Numero elementi senza max e min
Somma elementi senza max e min
Media elementi senza max e min
Varianza elementi senza max e min
Dev. Std elementi senza max e min
MAD elementi senza max e min
MSD elementi senza max e min
Valore massimo
Valore minimo
Numero elementi tra estremi non zero
Somma elementi tra estremi non zero
Media elementi tra estremi non zero
Varianza elementi tra estremi non zero
Dev. Std elementi tra estremi non zero
MAD elementi tra estremi non zero
MSD elementi tra estremi non zero
Posizione primo elemento non a zero
Posizione ultimo elemento non a zero
Mediana
Indicatori di process capability:
- CP
- CPL
- CPU
- CPK
- CPM
- CPKM
Funzioni vettoriali di una serie
Ritorno. (1)Inversione
Ordinamento crescente
Ordinamento decrescente
Cambio segno
Valore assoluto
Statistica Hotelling - In questo caso si passano le N serie di seguito. Il numero di variabili corrisponde al numero delle serie. Si deve passare inoltre, nel valore numerico 1, il numero di elementi di ogni serie e, nel valore numerico 2, il numero di variabili (attualmente è gestito solo il caso di 3 variabili). Il numero di elementi da passare è dato dal prodotto di questi due numeri.
Ad esempio, con le tre serie: 1,3,4,6; 4,2,5,8; 7,8,6,3, si passano i seguenti valori:
- Serie di input: 1,3,4,6,4,2,5,6,7,8,6,3
- N.elementi serie: 12
- Numeri di input: 4,3
Ritorna anche i seguenti numeri:
- n. elementi fuori limite
- limite della serie
Funzioni scalari di due serie
Numero elementi (1)Regressione lineare. Viene ritornata una coppia di numeri: l'ordinata all'origine e il coefficiente angolare della retta interpolatrice la spezzata costituita dalle due serie di input.
Media ponderata. Viene ritornata la media della prima serie pesata con i valori della seconda.
Media ponderata senza nulli. Vengono esclusi, dalla media ponderata, i valori nulli della prima serie
Deviazione tra due serie. Ritorna la radice quadrata del rapporto tra la somma dei quadrati delle differenze tra le due serie e il numero di elementi. E' utilizzata internamente, dal metodo Holt Winter, per stabilire la bontà della previsione, ed è stata quindi resa disponibile per un utilizzo pubblico. C'è da osservare che questa funzione rappresenta un'eccezione alla rappresentazione "geometrica" delle due serie, in quanto prevede che esse siano della stessa natura. Esse devono comunque avere lo stesso numero di elementi.
Funzioni vettoriali di due serie
Ritorna la prima serie (1)Ritorna la seconda serie (2)
Residuo della regressione. Calcola l'interpolazione e ritorna, per ogni elemento della serie, la differenza tra la prima serie e l'ordinata della retta interpolatrice (2)
Interpolazione multipla. Calcola l'interpolazione e ritorna, per ogni elemento della serie, il valore dell'ordinata della retta che interpola la prima serie (2)
Regressione multipla. Si deve impostare il numero di elementi della regressione, che è anche il numero degli elementi della serie di output.
Previsione con metodo Holt Winter (HW)
Implementa il metodo di previsione della domanda di Holt Winter, E' obbligatorio che le serie di input siano, esplicitamente o implicitamente, a passo unitario.
Devono essere impostati i seguenti dati di input:
- Periodicità; se non impostato si assume 12. Non può essere passato il valore 1 (viene ritornato errore)
- Alfa factor (fattore di smorzamento del livello); si imposta un valore tra 0 e 1.
- Beta factor (fattore di smorzamento del trend); si imposta un valore tra 0 e 1.
- Gamma factor (fattore di smorzamento della stagionalità); si imposta un valore tra 0 e 1.
Si può decidere di eseguire l'autofit solo su uno dei tre fattori; ad esempio, la seguente impostazione: Alfa=2; Beta=0,4; Gamma=0,9 indica che si desidera calcolare solo il valore migliore di Alfa.
Attenzione: è ammesso il valore 0, che fa sì che venga considerato solo il perido iniziale.
Un valore comunemente utilizzato è 0,2 per tutti e tre i coefficienti.
I valori degli indici calcolati, vengono ritornati nei numeri di output della routine.
- N. Periodi futuri di previsione; se non impostato viene assunta la periodicità
- Frontiera, ultimo periodo della serie di input che viene assunto come "passato". La previsione inizia dal periodo successivo. Se non impostato si assume il numero di periodi caricati. Se si imposta un valore superiore, viene ritornato errore.
- N.periodi di storia; numero di elementi della serie di input su cui eseguire la previsione, a partire dalla frontiera a ritroso: se non impostato si assume il numero periodi della frontiera. Se è maggiore di quest'ultima, e quindi sfonderebbe all'indietro, vengono assunti pari alla frontiera.
- Mantiene negativi; se impostato, nella serie ricevuta e nella previsione calcolata, vengono mantenuti i valori negativi. Il default è NO: nella serie di input, prima del calcolo, vengono azzerati i valori negativi, e che, se durante il calcolo della previsione dei periodi futuri, si ottiene un valore negativo, verrà anch'esso azzerato. La previsione che si calcola nel "passato", il cui scopo è di determinare i valori per arrivare alla frontiera, non viene invece mai azzerata.
- N.decimali di arrotondamento; se impostato un valore 0,1,2 o 3, la previsione viene arrotondata a questo valore. Se si imposta un valore diverso, non viene eseguito nessun arrotondamento.
- Autofit senza arretramento; normalmente, per eseguire l'autofit, è necessario disporre di una serie di almeno tre periodicità: impostando questo valore a 1, diventa sufficiente una serie di sole due periodicità.
- HW moltiplicativo; normalmente è utilizzato il metodo additivo, se si imposta a 1 questo valore, viene utilizzato il metodo moltiplicativo.
- Indice autofit; per determinare i migliori valori dei fattori di smorzamento, si deve scegliere, in questo campo, l'indice da minimizzare:
- 0 oppure ' ' (default) : Errore %
- 1 : Mape
- 2 : Errore di interpolazione
- 0 oppure ' ' (default) : Errore %
- N.periodi iniziali. Il metodo HW additivo, per determinare i valori iniziali di livello e trend, esegue un'interpolazione lineare sui primi elementi della serie. In questo campo si imposta il numero di periodi da trattare. Se non impostato, o impostato un valore maggiore della storia, si assume uguale a una periodicità. Se impostato un valore minore di due, si forza il valore due.
Viene ritornata una serie con un numero di elementi pari a quello delle serie di input sommato al numero di periodi di previsioni, riempita nei periodi di storia e in quelli di previsione con il valore della previsione calcolata.
Nei periodi di storia viene calcolata una previsione "passata" e viene confrontata con la serie storica, per ottenere indici di scostamento tra le due, che sono una stima dell'attendibilità della previsione "futura".
Coefficienti Holt Winters (HW)
Ritorna una serie di N elementi (dove N è tre volte la storia) contenente i coefficienti di livello, trend e stagionalità della sere HW predcedentemente calcolata, per ogni periodo della storia.
Ad esempio, con una storia di 24 periodi, la serie di output contiene:
- Posizioni 1 - 24 : livello degli elementi 1 - 24
- Posizioni 25 - 48 : trend degli elementi 1 - 24
- Posizioni 49 - 72 : stagionalità degli elementi 1 - 24
Vengono ritornati inoltre i seguenti numeri, che sono gli estremi delle tre sottoserie.
- Numero 1 - 1
- Numero 2 - 24
- Numero 3 - 25
- Numero 4 - 48
- Numero 5 - 49
- Numero 6 - 72
Questa funzione/metodo va lanciata dopo il calcolo Holt Winters.
Ritorna una serie di N elementi pari alla storia, che costituisce la statistica Hotelling della previsione. Ritorra anche i seguenti numeri:
- n. elementi fuori limite
- limite della serie
Implementa il metodo di previsione della domanda determinando la retta che interpola linearmente (con il metodo dei minimi quadrati) l'input, e calcolandone i valori per i punti di previsione. E' obbligatorio che le serie di input siano, esplicitamente o implicitamente, a passo unitario. Devono essere impostati i seguenti dati di input:
- Vedi HW. In questo metodo la periodicità non è utilizzatat direttamente. La si inserisce per omogeneità e per matenere gli stessi defalut di HW. Non viene dato errore se si passa il valore 1.
- N.S.
- N.S.
- N.S.
- Vedi HW
- Vedi HW.
- Vedi HW, con la differerenza che il numero minimo di periodi di storia è due.
- Vedi HW.
- Vedi HW
- N.S.
- N.S.
- N.S.
- N.S.
Vedi HW
Differenza tra serie 1 e serie 2
Ritorna una serie, in cui, in ogni elemento, viene calcolata la differenza tra il valore dello stesso elemento della serie 1 e della serie 2
Diferenza % tra serie 1 e serie 2
Ritorna una serie, in cui, in ogni elemento, viene calcolata la differenza tra il valore dello stesso elemento della serie 1 e della serie 2, divisa per il valore della serie 2, il tutto moltiplicato per 100. Se il valore della serie 2 è zero, viene ritornato zero.
Note:
(1) Oltre ad uno scopo didattico, questa funzione può essere utile in caso di caricamento progressivo. Si rimanda alla parte di documentazione tecnica per un'esposizione dettagliata
(2) Vengono ritornati anche, come scalari, l'ordinata all'origine e il coefficiente angolare della retta interpolarice
Utilizzo della /COPY
Funzione INZ (inizializzazione)
La si lancia una volta per comunicare che si sta per elaborare una nuova serie, ed il tipo di serie (singolo numero, semplice, doppia, ecc ...); in questa funzione si inizializzano:- le schiere interne del programma
- tutti i campi di input
- tutti i campi di output
Funzione CAR (caricamento)
La si lancia per caricare le serie di input; si passa il numero di elementi: se non impostato, si assume l'ultimo elemento non vuoto, si può richiamare più volte: i nuovi dati si accodano ai precedenti; in questa funzione si inizializzano (al ritorno del richiamo) i campi di input passati. La caratterizzazione alfanumerica di ogni elemento della serie è comune alle due serie: il valore viene messo nella posizione del numero corrispondente, e ricopre il precedente. Nel caricamento alternato si deve impostare, come numero di elementi, il numero di coppie. Ad esempio, se la prima serie è 1,2,3 e la seconda 8,7,6, per passarle con metodo A_12, si passa la serie 1,8,2,7,3,6, ed il numero di elementi 3.Deve esserci congruenza tra i metodi delle funzioni INZ e CAR
| Metodo INZ | Metodo CAR |
|---|---|
| NUM | A_N |
| SIN | A_1 |
| DOP | A_1 |
| DOP | A_2 |
| DOP | A_12 |
| DOPUNI | A_1 |
Negli altri casi viene acceso l'indicatore 35 e ritornato il messaggio di incongruenza tra inizializzazione e caricamento.
Funzione Fxx (esecuzione funzione)
Al primo richiamo si deve SEMPRE pulire il messaggio £G56MS. Anche in questo caso si controlla la congruenza tra la funzione di inizializzazione e di esecuzione.Deve esserci congruenza tra il metodo della funzione INZ e la funzione di calcolo Fxx
| Metodo INZ | Funzione Fxx |
|---|---|
| NUM | F01 F02 |
| SIN | F03 F04 |
| DOP | F03 (*) F04 (*) F05 F06 |
| DOPUNI | F03 (*) F04 (*) F05 F06 |
(*): funzioni eseguite sulla prima serie delle due
Negli altri casi viene acceso l'indicatore 35 e ritornato il messaggio di incongruenza tra inizializzazione ed esecuzione.
Si passano i dati di input specifici della funzione (numeri e e stringa, che vengono puliti dopo il richiamo). Questa impostazione ha l'effetto di inizializzare tutti i campi di output. Se la serie di output non è finita (ha un numero di elementi maggiore di quello della schirea di passaggio) viene tornato il messaggio CONT: occorre richiamare la routine (con la stessa funzione), lasciando il messaggio CONT. Negli altri casi ritorna il messaggio vuoto. La schiera dei numeri e dei significati (come effetto collaterale di un ritorno di un vettore) viene ritornata tutte le volte. Idem per la stringa di output.
Descrizione formule utilizzate
F01102 - Valore attuale
Attualizzazione di un valore: dato un montante (valore finale), la data iniziale e finale, e un valore di interesse, viene ritornato il valore attualizzato, che porta al montante, in caso di interesse composto su base annuale.::FIG M(B£MATE) P(B£MATE_A) R(60) A(C)
F03300 - Numero Elementi
È il numero di elementi della serie. Se è il caso, questo valore tiene conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli). F03301 - Somma
È la somma degli elementi della serie. Se è il caso, questo valore tiene conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli). F03302 - Media
È la media degli elementi della serie. Se è il caso, questo valore tiene conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli). F03303 - Varianza
Si indica con S2 (esse quadro).È data dalla somma dei quadrati delle differenze tra ogni valore della serie e il valor medio della serie, divisa per il numero degli elementi della serie meno uno. È un indice della dispersione dei valori della serie attorno al valore medio: è espressa in un'unità di misura pari alla seconda potenza di quella della serie. Per questo motivo si preferisce l'utilizzo della deviazione standard, che è pari alla sua radice, e che quindi è nella stessa unità di misura della serie. Se è il caso, viene calcolato con i valori che tengono conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli).
::FIG M(B£MATE) P(B£MATE_S2) R(60) A(C)
F03304 - Deviazione standard
Si indica con S (esse).È data dalla somma dei quadrati delle differenze tra ogni valore della serie e il valor medio della serie, divisa per il numero degli elementi della serie meno uno, il tutto posto sotto radice quadra. È un indice della dispersione dei valori della serie attorno al valore medio: è espressa nella stessa unità di misura della serie. Corrisponde alla radice quadrata della varianza. Suoi sinonimi sono: "Scarto tipo", "Scarto quadratico medio", "Sigma". Se è il caso, viene calcolato con i valori che tengono conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli).
Con questa formula viene calcolata la deviazione standard con correzione di Gauss.
::FIG M(B£MATE) P(B£MATE_S) R(60) A(C)
F03305 - MAD
È l'acronimo di mean absolute deviation (deviazione media assoluta). tra i dati e la media. È data dalla somma del valore assoluto delle differenze tra ogni valore della serie e il valor medio della serie, divisa per il numero degli elementi della serie. Rappresenta lo scostamento medio (in valore assoluto) dei valori della serie rispetto alla media, ed è espresso nella stessa unità di misura della serie. Se è il caso, viene calcolato con i valori che tengono conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli).::FIG M(B£MATE) P(B£MATE_MAD) R(60) A(C)
F03306 - MSD
È l'acronimo di mean squared deviation (deviazione media quadratica). tra i dati e la media. È data dalla somma dei quadrati delle differenze tra ogni valore della serie e il valor medio della serie, divisa per il numero degli elementi della serie. Se è il caso, viene calcolato con i valori che tengono conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli).::FIG M(B£MATE) P(B£MATE_MSD) R(60) A(C)
F03307 - CV
È l'acronimo di Coefficiente di Variazione tra i dati e la media. È dato dal rapporto, moltiplicato per 100, tra la deviazone standard ed il valore assoluto della media. Essendo una percentuale, dà un'idea immediata della deviazione standard, indipendentemente dalla sua unità di misura.Se è il caso, viene calcolato con i valori che tengono conto dei "tagli" alla serie (senza zeri, senza massimo e minimo, tra estremi non nulli).
F03360 - Mediana
Si ordina la serie: se ha un numero di elementi dispari si prende il valore centrale; se ha un numero di elementi pari si prende la media dei due valori centrali. F03361 - CP
Stima la capacità del processo considerando che la media sia centrata tra 2 limiti inferiore e superiore delle specifiche. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale.::FIG M(B£MATE) P(B£MATE_CP) R(60) A(C)
F03362 - CPL
Stima la capacità del processo considerando se la specifica consiste solo del limite inferiore. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale.::FIG M(B£MATE) P(B£MATE_CPL) R(60) A(C)
F03363 - CPU
Stima la capacità del processo considerando se la specifica consiste solo del limite superiore. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale.::FIG M(B£MATE) P(B£MATE_CPU) R(60) A(C)
F03364 - CPK
Stima la capacità del processo considerando che la media potrebbe NON essere centrata tra 2 limiti inferiore e superiore delle specifiche. (Se la media non è centrata CP sovrastima la capacità del processo). CPK < 0 quando il processo cade al di fuori dei limiti di specifica. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale.::FIG M(B£MATE) P(B£MATE_CPK) R(60) A(C)
F03365 - CPM
Stima la capacità del processo attorno ad un obiettivo (target T). CPM è sempre > 0. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale. È anche conosciuto come indice di capacità TAGUCHI::FIG M(B£MATE) P(B£MATE_CPM) R(60) A(C)
F03366 - CPKM
Stima la capacità del processo attorno ad un obiettivo (target T) e considera che la media non sia centrata tra i limiti. Si assume che il risultato del processo sia distribuito secondo una distribuzione normale.::FIG M(B£MATE) P(B£MATE_012) R(60) A(C)
F06612 - Accuracy
Per ogni elemento della serie si calcola il modulo della differenza percentuale tra la serie 2 e la serie 1, e se ne calcola il complemento a 100, portando a zero i valori negativi.Se i valori sono uguali l'accuracy è 100. Se l'errore percentuale è maggiore del 100% l'accuracy è 0. Questo indice quindi "appiattisce" gli scostamenti elevati.
Algoritmo del sacco
Algoritmo 1 del sacco: dato un insieme di N elementi ed un valore M, determinare il sottoinsieme di N la cui somma si avvicina maggiormente a M senza superarlo.Algoritmo 2 del sacco, o della suddivisione bilanciata: dato un insieme di N elementi ed un valore M, suddividere in M sottoinsiemi tali che le loro somme siano le più omogenee possibili.
Descrizione tecnica.
La £G56 va richiamata tre volte di seguitoPrimo richiamo (comune)
- £G56FU='INZ'
- £G56ME='SIN'
Secondo richiamo (comune)
- £G56FU='CAR'
- £G56ME='A_1'
Terzo richiamo per il sacco
- £G56FU='F04'
- £G56ME='409'
In £G56IN(2) si passa il numero dei decimali (default zero)
In £G56IN(3) si passa 1 se si vogliono tornare i valori, si lascia a zero se si vogliono i puntatori (è il ritorno naturale del sacco)
Ritorna
In £G56OS il numero di elementi
In £G56OV la schiera (di puntatori agli elementi utilizzati o i loro valori a seconda della scelta)
In £G56ON(1) il valore di riempimento a cui è arrivato
In £G56ON(2) il numero di elementi che ha utilizzato
Terzo richiamo per la suddivisione bilanciata
- £G56FU='F04'
- £G56ME='410'
In £G56IN(2) si passa il numero dei decimali (default zero)
Ritorna
In £G56OS il numero di elementi (uguale a quello di input)
In £G56OV la schiera della posizione in cui ha posto l'elemento di input.
In £G56ON(X) date M le suddivisioni, contiene nelle posizioni da 1 a M la somma degli elementi per ogni posizione, nelle posizioni da M+1 a 2M il numero di elementi di ogni posizione.
Note
Il valore massimo di ogni elemento dell'insieme di partenza e del riempimento del sacco è di 18.000, per motivi di ampiezza massima di un'area di memoria indirizzabile.Quando questo valore viene superato viene ritornato un messaggio d'errore e l'elaborazione termina.
Dato che la routine al suo interno tratta solo numeri interi, in presenza di decimali va impostato il numero di decimali da trattare. È da tener presente che è questo valore che va confrontato con il valore massimo. Ad esempio, un valore 19,321 con impostati tre decimali viene scartato, in quanto all'interno del programma viene trasformato in 19321.
Vengono eseguiti due controlli di sfondamento.
Il primo che la soglia di riempimento non superi il valore massimo (messaggio BAS1348).
Il secondo che nessun elemento dell'insieme di input superi il valore massimo (messaggio BAS1349).
Previsioni con HW
Sono stati realizzati nuovi passi MPS che implementano il calcolo della previsione con metodo HW Previsioni con Holt Winters
Introduzione
Questo passo calcola, a partire da una vista di input(vista storica)la previsione futura con il metodo di Holt Winters (nel seguito HW) e ne memorizza il risultato nella vista di output(vista previsioni). NB; nella vista di output oltre alle previsioni nei periodi futuri vengono calcolate anche le previsioni HW relative alla storia (in questo modo è possibile ad esempio l'applicazione dell'autofit senza arretramento e per il calcolo del coefficiente di bontà della previsione).Per una esposizione dettagliata del metodo HW:
Previsioni con Holt Winters
Impostazioni
Il piano deve essere a periodi omogenei (a mesi, settimane, ecc..). Tutti i valori da impostare (periodi di previsione, di storia, ecc..) vanno impostati in questa unità di misura. Periodicità
E' un campo obbligatorio. Si imposta il numero di periodi dopo i quali la serie assume, approssimativamente, lo stesso valore. Ad esempio, una periodicità di 12 mesi indica che la forma della serie si ripete (con picchi e valli) dopo questo intervallo. Frontiera
E' un campo obbligatorio. Si imposta l'ultimo periodo che, nella serie di input, viene considerato "nel passato". La previsione inizia ad essere calcolata dal periodo successivo. Numero periodi di previsione
E' un campo obbligatorio. Indica il numero di periodi, a partire da quello successivo alla frontiera, per cui si calcola la previsione. La somma dei periodi di previsione e della frontiera non può superare 120, per non sfondare i periodi del piano. Questo controllo implica che sia la frontiera sia la previsione siano, singolarmente, minori di questo valore. Numero periodi di storia
E' un campo obbligatorio. Indica il numero di periodi, a partire dalla frontiera all'indietro, che vengono utilizzati per la determinazione dei parametri di calcolo del metodo. Non può quindi essere maggiore della frontiera, altrimenti provocherebbe uno sfondamento nel passato.Non può essere minore della periodicità aumentata di 1, in HW additivo, e di due volte la periodicità, in HW moltiplicativo. Una storia più estesa (e quindi almeno di due periodicità) smorza gli effetti della stagionalità.
Numero periodi iniziali
E' un campo facoltativo: se non impostato, si assume pari alla periodicità. Deve essere maggiore di 1 e minore o uguale alla storia. Indica il numero di periodi su cui si esegue l'interpolazione per determinare i valori iniziali di livello e trend, necessari per il calcolo. Un valore vicino ad 1 rafforza i periodi iniziali, un valore vicino alla storia considera tutti i periodi in modo più uniforme. Esempio di impostazione periodi
Con i seguenti valori:- Frontiera = 35
- N. Periodi di Storia = 24
- N. Periodi di Previsione = 12
- Storia: dal periodo 12 al 35 (estremi compresi)
- Previsione: dal periodo 36 al periodo 47 (estremi compresi)
Fattori di smorzamento
Alfa, Beta, GammaIndicano il peso, all'interno della storia, dei periodi più recenti rispetto a quelli più remoti, rispettivamente per il livello, il trend e la stagionalità. Il loro valore va da 0 (conta solo il primo periodo) ad 1 (conta solo l'ultimo periodo). Per ognuno di essi si può, in modo indipendente dagli altri due:
- impostare il campo di autofit (in modo che il sistema calcoli il valore ottimo)
- lasciare in bianco l'autofit e impostare un valore tra 0 (il che corrisponde a utilizzare solo il periodo iniziale) e 1 (il che corrisponde a utilizzare solo il periodo finale). Il default se il campo non è impostato è 0.
Nota Bene; il campo autofit e il valore sono alternativi: se il valore è impostato l'autofit deve essere blank.
A seconda delle versioni installate, se impostato il campo autofit può assumere valori:
- 1 = attivo autofit, il sistema itera il calcolo con valori di incremento del fattore di smorzamento a passo 0,2: valori 0 - 0,2 - 0,4 - 0,6 - 0,8 - 1
- da 2 a 9 = autofit con passo variabile, il passo di incremento del fattore di smorzamento viene calcolato dividendo l'intervallo tra 0 e 1 in un numero pari a quello inserito nel campo, il calcolo viene iterato incrementando di volta in volta il fattore di smorzamento con un valore pari al passo calcolato
Autofit senza arretramento
Se si imposta di calcolare almeno uno dei tre fattori di smorzamento, e la storia non vale almeno tre periodicità, deve essere impostato questo campo, e quindi eseguire il test direttamente sul periodo di previsione. In assenza di questa impostazione si devono poter ritagliare due periodicità di training ed una di test. A rigore, per l'HW additivo, sarebbero sufficienti due periodicità più uno, ma si è preferito avere un periodo di training più robusto. HW Moltiplicativo
Se impostato, la previsione verrà eseguita con il metodo moltiplicativo, (più sensibile alla variazioni stagionali). Se invece si lascia in bianco, verrà utilizzato il metodo additivo (impostazione consigliata). Mantiene negativi
Il calcolo può produrre valori di previsione negativi. Se impostato questo valore, essi, nella parte di previsione effettiva (oltre la frontiera) verranno mantenuti, se invece viene lasciato vuoto, verranno portati a zero. Nella parte storica (previsioni dall'inizio della storia alla frontiera) i negativi vengono sempre mantenuti, essendo valori utilizzati nel calcolo dello scostamento tra realtà e previsione, e quindi un loro azzeramento implicherebbe una riduzione arbitraria dello scostamento stesso. N. Decimali di arrotondamento
Se impostato un valore da 0 a 3, si esegue l'arrotondamento per il numero corrispondente di decimali. A differenza dell'azzeramento dei negativi, l'arrotondamento viene eseguito su tutta la previsione, sia effettiva sia storica. Indice autofit
Se impostato il calcolo dei fattori di smorzamento tramite autofit, in questo campo si seleziona l'indice di confronto per stabilire la migliore previsione, tra i tre valori calcolati e memorizzati nei numeri dell'MPS:- % di errore (default)
- Mape
- Sigma
Memorizzazione numeri
E' possibile memorizzare, sia i numeri di dettaglio sia i numeri di riepilogo, su appositi record di D5COSO.Con questo campo si può impostare di:
- ' ' Memorizzare sia i numeri di dettaglio sia i numeri di riepilogo
- '1' Memorizzare solo i numeri di dettaglio
- '2' Memorizzare solo i numeri d riepilogo
- '3' Non memorizzare i numeri
Numeri di dettaglio
Sono memorizzati dopo aver calcolato le previsioni di ogni articolo. Per la loro memorizzazione, devono verificarsi le seguenti condizioni:- Le viste devono avere il codice 1 di tipo AR e il codice 2 o vuoto o di tipo TAMAG.
- Se l'applicazione è multiplant, nel codice piano deve essere impostato il plant (A), oppure il plant è il codice 2 della vista (B).
Numeri di riepilogo generali
Sono memorizzati al termine del calcolo delle previsoni di tutti gli articoli. Il contesto è TAMPC (codice vista) ed il tema £P2 (del sottosettore MP). Il codice 1 è il piano. Il campo data / periodo è lasciato vuoto, in quanto la coppia vista / piano è univoca. Numeri di riepilogo per plant.
Sono memorizzati al termine del calcolo delle previsoni di tutti gli articoli se l'applicazione è multiplant. Il contesto è TAMPC (codice vista) ed il tema £P3 (del sottosettore MP). Il codice 1 è il piano. Il codice 2 è il plant, ripreso dal plant del piano nel caso (A) e dal plant del record nel caso (B). Il campo data / periodo è lasciato vuoto, in quanto la coppia vista / piano è univoca. Vista di statistica Hotelling
Per ogni record di previsione viene scritta una vista che riporta la statistica Hotelling, allo scopo di analizzare la prevedibilità della serie. Il piano è lo stesso delle previsioni. La vista, di codice fisso £P1 (elementi del settore MPC che viene costruito automaticamente al primo richiamo), ha la stessa tipizzazione delle viste di storia e di previsioni (primo codice fisso "AR" e secondo codice o bianco o "TAMAG"). Essa riporta il valore della statistica per ogni elemento della storia. Ad esempio, con una frontiera al periodo 36, ed una storia di 24 periodi, sono valorizzati gli elementi dal 13 al 36 della vista £P1. Vengono inoltre valorizzati i primi quattro numeri del record della vista:- Nel primo numero, il numero di elementi che superano il limite. E' sufficiente che il limite sia superato una sola volta, perchè la serie non sia prevedibile.
- Nel secondo numero, il valore limite (che dipende dal numero di periodi della storia)
- Nel terzo numero, il primo periodo della storia (primo periodo siginificativo della vista MPS di Hotelling).
- Nel quarto numero, l'ultimo periodo della storia (ultimo periodo siginificativo della vista MPS di Hotelling).
Previsioni con Regressione lineare
Introduzione
Questo passo calcola, a partire da una vista di input(vista storico)la previsione futura, con il metodo della regressione lineare.Si determina la retta che meglio interpola la vista di input, minimizzandone la distanza con i valori della vista, e su di essa si calcolano ii valori della vista di output(vista previsioni).
Impostazioni
Il piano deve essere a periodi omogenei (a mesi, settimane, ecc..). Tutti i valori da impostare (periodi di previsione, di storia, ecc..) vanno impostati in questa unità di misura. Frontiera
E' un campo obbligatorio. Si imposta l'ultimo periodo che, nella serie di input, viene considerato "nel passato". La previsione inizia ad essere calcolata dal periodo successivo. Numero periodi di previsione
E' un campo obbligatorio. Indica il numero di periodi, a partire da quello successivo alla frontiera, per cui si calcola la previsione. La somma dei periodi di previsione e della frontiera non può superare 120, per non sfondare i periodi del piano. Questo controllo implica che sia la frontiera sia la previsione siano, singolarmente, minori di questo valore. Numero periodi di storia
E' un campo obbligatorio. Indica il numero di periodi, a partire dalla frontiera all'indietro, che vengono utilizzati per la determinazione dei parametri di calcolo del metodo. Non può quindi essere maggiore della frontiera, altrimenti provocherebbe uno sfondamento nel passato. Esempio di impostazione periodi
Con i seguenti valori:- Frontiera = 35
- N. Periodi di Storia = 24
- N. Periodi di Previsione = 12
- Storia: dal periodo 12 al 35 (estremi compresi)
- Previsione: dal periodo 36 al periodo 47 (estremi compresi)
Mantiene negativi
Il calcolo può produrre valori di previsione negativi. Se impostato questo valore, essi, nella parte di previsione effettiva (oltre la frontiera) verranno mantenuti, se invece viene lasciato vuoto, verranno portati a zero. Nella parte storica (previsioni dall'inizio della storia alla frontiera) i negativi vengono sempre mantenuti, essendo valori utilizzati nel calcolo dello scostamento tra realtà e previsione, e quindi un loro azzeramento implicherebbe una riduzione arbitraria dello scostamento stesso. N. Decimali di arrotondamento
Se impostato un valore da 0 a 3, si esegue l'arrotondamento per il numero corrispondente di decimali. A differenza dell'azzeramento dei negativi, l'arrotondamento viene eseguito su tutta la previsione, sia effettiva sia storica. Previsioni con scelta metodo
Questo passo calcola la previsione futura scegliendo il metodo
Previsioni: Correzione serie
Nel processo di previsione spesso è necessario apportare correzioni alle serie coinvolte nel processo.Ad esempio, in caso di sostituzione di un articolo, se essa è avvenuta nel passato, ma comunque all'interno del periodo su cui si basano le previsioni, si deve conglobare la storia dell'articolo sostituito in qella del sostituente, mentre, se avverrà nel futuro, si dovrà, a partire dal periodo di cambio, sostiture la previsione dell'articolo sostituito, con quella del sostituente.
Inoltre, una serie di input che rappresenta il consuntivo delle vendite, potrebbe essere sottoposta ad un "lisciamento", che taglia i picchi anomali, oppure all'eliminazione degli effetti di una promozione, prima di essere utilizzata nella generazione della previsione.
Questo passo esegue la seguente funzione:
- data una vista di input e una serie di azioni, determina una vista di correzioni, ed una vista di output che è la somma algebrica delle due precedenti.
- la vista di correzione ha unicamente uno scopo documentativo, isolando le correzioni, che vengono "annegate" nella vista di output.
- la serie di azioni è contenuta in uno script (Par. di scelta) risiedente in SCP_SET: per default viene assunto il membro MPAP53.
- ogni azione esegue una correzione specifica (lisciamento, sostituzione, ecc...)
- le tre viste (input, correzione e output) sono tutte obbligatorie (e necessariamente diverse tra loro) e intestate alla stessa copia di oggetti.
E' quindi necessario fornire alcune caratteristiche della vista di input, utilizzate dai passi di correzione:
- Si deve inserire (obbligatoriamente) la frontiera (ultimo periodo della storia). Questa informazione (statica) insieme al piano (rolling) permette di stabilire dinamicamente se la sostituzione di un codice è avvenuta nel passato oppure avverrà nel futuro.
- Si deve inoltre specificare se la serie di input è una serie storica od una serie di previsioni. In questo modo è possibile condizionare un'azione (ad esempio di lisciamento): farla eseguire solo se la serie è storica, senza dover duplicare gli script.
- Bisogna inoltre impostare anche il numero di periodi di storia (per default assume la frontiera) e il numero di periodi di previsione.
- Per la serie storica dall'inizio della storia alla frontiera
- Per la serie di previsioni dal periodo successivo alla frontiera fino al numero di periodi di previsioni.
Sostituzione articolo
Si inserisce nello script (default MPAP53 di SCP_SET) il passo ..M53_01Il legame tra sostituto e sostituente si inserisce nel tipo distinta fisso £CS, in cui gli oggetti sono entrambi articoli.
E' possibile utilizzare un tipo distinta diverso specificandolo all'interno dello script in posizione 10-11-12 (Es.: ..M53.01 XXX utilizzo del tipo distinta XXX).
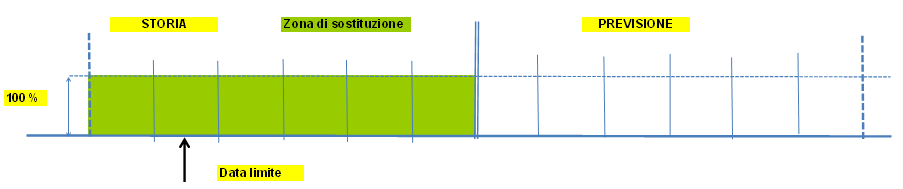
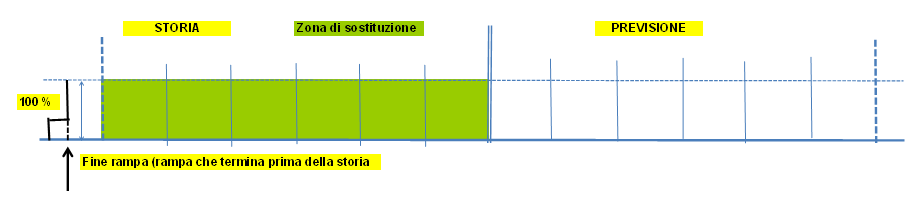
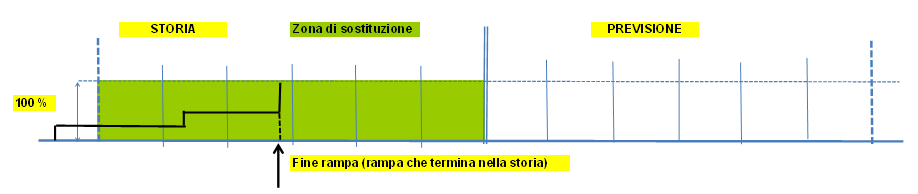
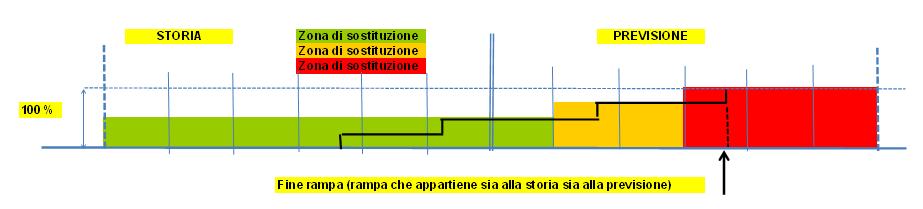
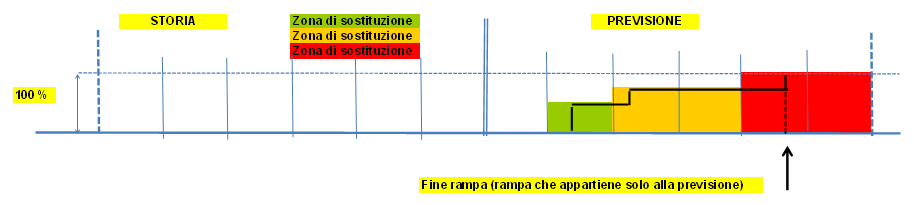
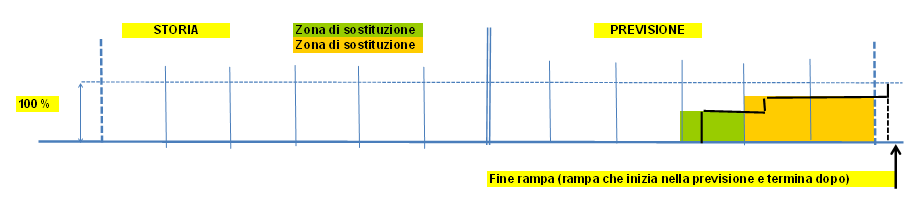
L'assieme è il codice sostituito; il componente è il codice sostituente; la quantità di legame è la percentuale di sostituzione; la data di inizio validità (opzionale) è il punto in cui avviene la sostituzione, in caso di sostituzione a rampa; dalla data si risale al periodo MPS a cui essa appartiene, una data a zero ha il significato di sostituzione "da sempre" nel passato.
E' gestita la sostituzione uno a uno: viene considerato solo il primo componente. Ovviamente nel caso di sostituzione a rampa esso va ripetuto, ma viene comunque considerato solo il primo codice.
Sono implementati i seguenti assunti e forzature:
- Non è importante che i legami siano in data crescente: il sistema li riordina.
- I coefficienti di impiego maggiori di 1, e quello dell'ultimo periodo di rampa, vengono portati a 1.
- Non viene controllato che essi siano crescenti per data.
- Se vi è più di un legame nello stesso periodo, viene trattato quello con la data più alta.
- Se vi sono sia legami senza data sia legami con data, i primi vengono eliminati.
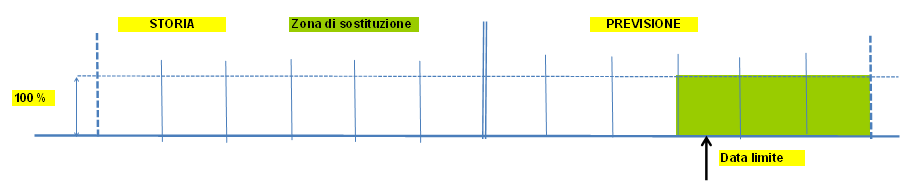
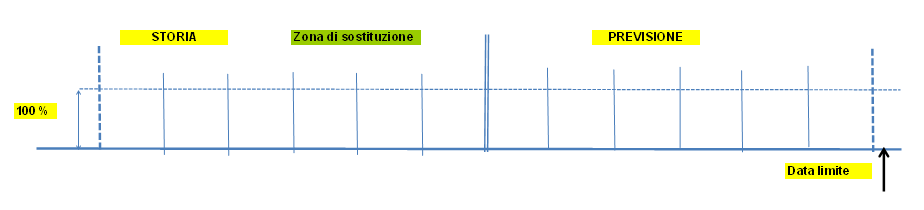
Esempi grafici di sostituzione
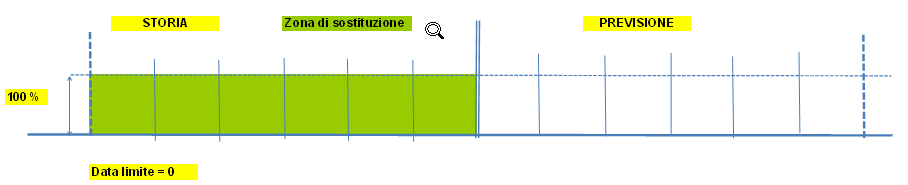 |
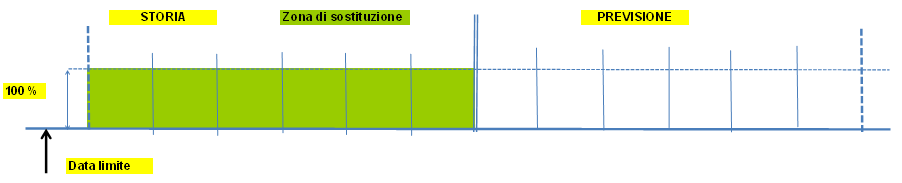 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
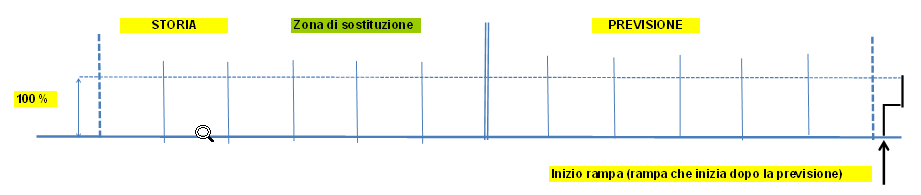 |
Sostituzione articolo 1 -> N
Si inserisce nello script (default MPAP53 di SCP_SET) il passo ..M53_03Il legame tra sostituto e sostituenti si inserisce nel tipo distinta di default £CN in cui gli oggetti sono entrambi articoli. E' possibile utilizzare un tipo distinta diverso specificandolo all'interno dello script in posizione 10-11-12 (Es.: ..M53.03 SOS utilizzo del tipo distinta SOS).
L'assieme è il codice sostituito; il componente è il codice sostituente; la data di inizio validità è il punto in cui avviene la sostituzione (data a zero ha il significato di sostituzione "da sempre" nel passato).
Nell'inserimento della distinta deve essere tenuto in considerazione l'accorgimento che le date di validità dei sostituenti allo stesso livello devono essere uguali.
Il processo di sostituzione si comporta in modo diverso a seconda che la sostituzione sia nel passato o nel futuro.
Sostituzione nel passato
I sostituenti sono individuati leggendo la distinta di sostituzione riepilogata ai materiali base con data di validità uguale alla data fine della frontiera (ultimo periodo della storia). Sostituzione nel futuro
I sostituenti sono individuati leggendo la distinta di sostituzione con il programma di interfaccia B£IDIBM creato allo scopo di scandire ed elaborare le distinte di sostituzione. La data di inizio validità è la data inizio del primo periodo successivo alla frontiera.E' possibile utilzzare il programma TSTDIBM, che presenta questa scansione a video.
Esempio grafici di sostituzione
Distinta di sostituzione dell'assieme A01.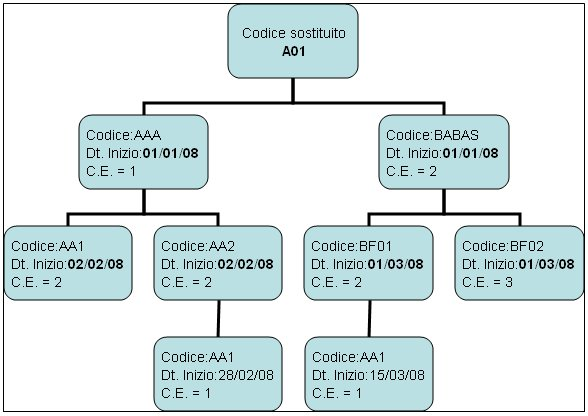 |
Sostituzione nel passato considerando come data fine della frontiera (ultimo periodo della storia) il 29/02/2008.
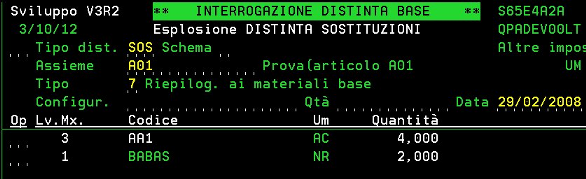 |
Sostituzione nel futuro considerando come data di inizio (inizio del primo periodo successivo alla frontiera) il 01/03/2012.
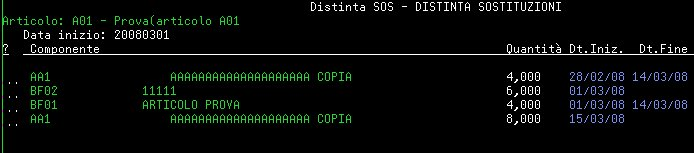 |
Indici Previsioni articolo
Per la previsione HW sono stati scritti nuovi indici di D5COSO. Sono stati quindi modificati i programmi generali di rifasatura contesti e temi, i programmi contenenti la descrizione degli indici, e la documentazione degli indici. Descrizione Indici Previsioni articolo
** - Documentazione generale del tema
Questo tema ha lo scopo di registrare i valori calcolati dalla previsione,Sono valori relativi ad ogni singolo articolo
01 - MAPE consuntivo
È il MAPE (Mean absolute percentage error) calcolato, nella parte storica, a partire dai valori della previsione della storia.È un dato significativo per determinare la classe previsionale
02 - SIGMA consuntivo
È il SIGMA (Deviazione standard) calcolato, nella parte storica, a partire dai valori della previsione della storia. 03 - Errore % Consuntivo
È l'errore % calcolato, nella parte storica, a partire dai valori della prevision e della storia. 04 - Numero toccate
È il numero di valori diversi da zero nella parte storica. Al massimo coincide con la storia.È un dato significativo per determinare la classe previsionale
05 - Classe previsionale
È un valore che indica l'attendibilità della previsione.Si calcola in base al Mape e al numero di toccate, e ad una griglia di impostazioni registrata in tabella MP2 (elemento '*')
06 - Profondità della storia
È la posizione, nella storia, del primo elemento diverso da zero.Ad esempio, se il primo elemento diverso da zero è il terzultimo, la serie ha una profondità di 3.
È un dato significativo per la determinazione della classe previsionale.
Se è al di sotto di una soglia impostata in tabella MP2, viene assegnata la classe più bassa.
07 - Max alfa,beta,gamma
È il valore maggiore tra i tre coefficiente di smorzamento utilizzato nella previsione.È un dato di input nel calcolo dell'incertezza a N passi.
08 - Giorni a lead time
Si parte dall'inizio del periodo successivo alla frontiera (data inizio previsione) e ci si sposta in avanti del lead time della politica master dell'articolo (fisso + variabile + rettifica).Per l'avanzamento del periodo si utilizzano i giorni solari o quelli di calendario in base a quanto impostato in tabella M51 per la politica master.
La differenza tra queste date viene registrata in questo campo.
09 - Giorni a fine periodo
Si avanza la data calcolata nell'indice 8 fino alla prima fine periodo. La differenza tra questa data e la data inizio previsione viene registrata in questo campo. 10 - Passo
È il periodo in cui cade la data calcolata nell'indice 9 11 - Incertezza a N passi
È il sigma (incertezza) calcolata per il periodo determinato nell'indice 10. |
12 - Incertezza proporzionale
È data dall'indice 11 moltiplicato per l'indice 8 e diviso per l'indice 9.È il valore utilizzato (moltiplicato per il coefficiente K in funzione del livello di servizio desiderato) per la scorta calcolata.
13 - Data sfondamento
Se la data calcolata nell'indice 8 supera la data finale del piano, viene assunta come data per i calcoli quest'ultima, ed in questo indice viene registrata l'effettiva data, a scopi documentativi, e come segnalazione di possibili incongruenze. 14 - N.elementi fuori limite
È il numero di elementi della statistica Hotelling di questa serie che superano il valore limite (registrato nell'indice 15) 15 - Valore limite
È il valore limite della serie Hotelling, al di sopra del quale la serie originale non ha un comportamento stabile.Nel caso di previsioni HW dipende unicamente dal numero di periodi della storia.
Classe previsiva articolo
Ad ogni articolo/plant oggetto di previsione, viene assegnata una classe previsiva in base alle impostazioni immesse in tabella MP2 (settore **). La classe previsiva viene ritornata come OAV dell'articolo/plant, e come OAV dell'articolo (nel planti di competenza). Scorta minima e calcolo / utilizzo scorta minima dinamica
Come "sottoprodotto" della previsione HW è stato implementato il calcolo dinamico della scorta minima, che è stato utilizzato nell'analisi disponibilità (nel ritorno della scorta minima e della scorta datata). La routine £GMA di ritorno dati articolo/plant può ricevere il parametro di modalità di calcolo e risalita scorta minima. E' stato realizzato un nuovo OAV per la scelta della risalita Scorta minima
Introduzione
La scorta minima è un fabbisogno indipendente, che individua la quantità della giacenza che si desidera avere a disposizione per coprire necessità impreviste. Da un punto di vista statistico, è una stima dell'incertezza della domanda: un articolo la cui storia dei consumi è "stabile", sarà maggiormente prevedibile di un altro con storia più "erratica", e quindi richiederà una scorta minore di quest'ultimo, a pari livello di precisione richiesto. E' quindi comprensibile come la scorta minima possa essere determinatata a partire da informazioni "collaterali" di un processo previsivo effettuato con metodi matematici (nel nostro caso l'algoritmo di Holt Winters). Impostazione in dati articolo / plant
In questo archivio è possibile immettere direttamente la scorta minima, e/o impostare che essa verrà determinatata automaticamente dalle previsioni. Per abilitare questa seconda modalità, è necessario inserire, nel campo "Calcolo scorta lotti" del formato di manutenzione dati articolo/plant, il valore fisso "£01". Questo campo è un elemento dealla tabella GMS inserito automaticamente, se inesistente, all'ingresso del programma di manutenzione dati articolo/plant. Priorità di scelta
Se sono state inserite sia la scorta manuale, sia l'impostazione di calcolare la scorta, è possibile, nei luoghi dove è richiesto il ritorno della scorta, impostare la priorità di scelta, che può assumere uno dei valori dell'oggetto V2/GM_RS.Risalita scorta minima
Modalità di calcolo scorta
Il calcolo Holt Winters determina un valore di previsione anche per ogni periodo della storia. Viene quindi calcolato l'errore di interpolazione (Sigma) tra i due valori, ottenuto come radice della differenza quadratica media (sommatoria dei quadrati delle differenze tra previsione e storia, divisa per il numero dei periodi della storia). Il Sigma rappresenta l'incertezza "a un passo", vale a dire quella relativa al primo periodo di previsione (quello immediatamente successivo alla frontiera). In realtà, in base al lead time dell'articolo in esame, può darsi che si debba considerare l'incertezza "a N passi", che sarà sicuramente maggiore.Il metodo di calcolo è il seguente:
NB: tutti i valori citati nel seguito sono registrati nel tema £P1 dell'archivio D5COSO del contesto articolo, alla data di inizio pevisione.
- Si parte dalla data di inizio del primo periodo dopo la frontiera D1 e, avanzando del lead time della politica master dell'articolo, per una quantità pari al Sigma, si trova una nuova data D2.
- Si trova il periodo in cui cade questa data, e la sua distanza della frontiera è il numero di passi N che si utilizza nel seguito.
- Si calcolano poi i giorni G1 tra D2 E D1, e quelli G2 tra D3 (data di fine del periodo a cui appartiene D2) e D1.
- Se la data D3 sfonda l'ultimo periodo del piano, viene assunta quest'ultima data, e viene registrata la D3 nel tema £P1, nel campo data sfondamento.
- Si calcola quindi il Sigma a N passi, secondo la formula di Hen Siong Tan (registrato nel campo incertezza a N passi).
- Si determina infine l'incertezza proporzionale, moltiplicando l'incertezza a N passi per il rapporto tra G2 e G1.
- Per ottenere la scorta minima si deve decidere il livello di servizio che si desidera assicurare; il livello di servizio è un valore tra zero ed uno (estremi esclusi). Un valore pari a zero comporta una scorta anch'essa zero, un valore pari a uno, comporta una scorta infinita; il livello di servizio dipende dalla classe previsiva, calcolata per ogni articolo, secondo i parametri impostati in tabella MP2.
MP2 - Parametri previsioni HW
Valori consigliati per la tabella MP2
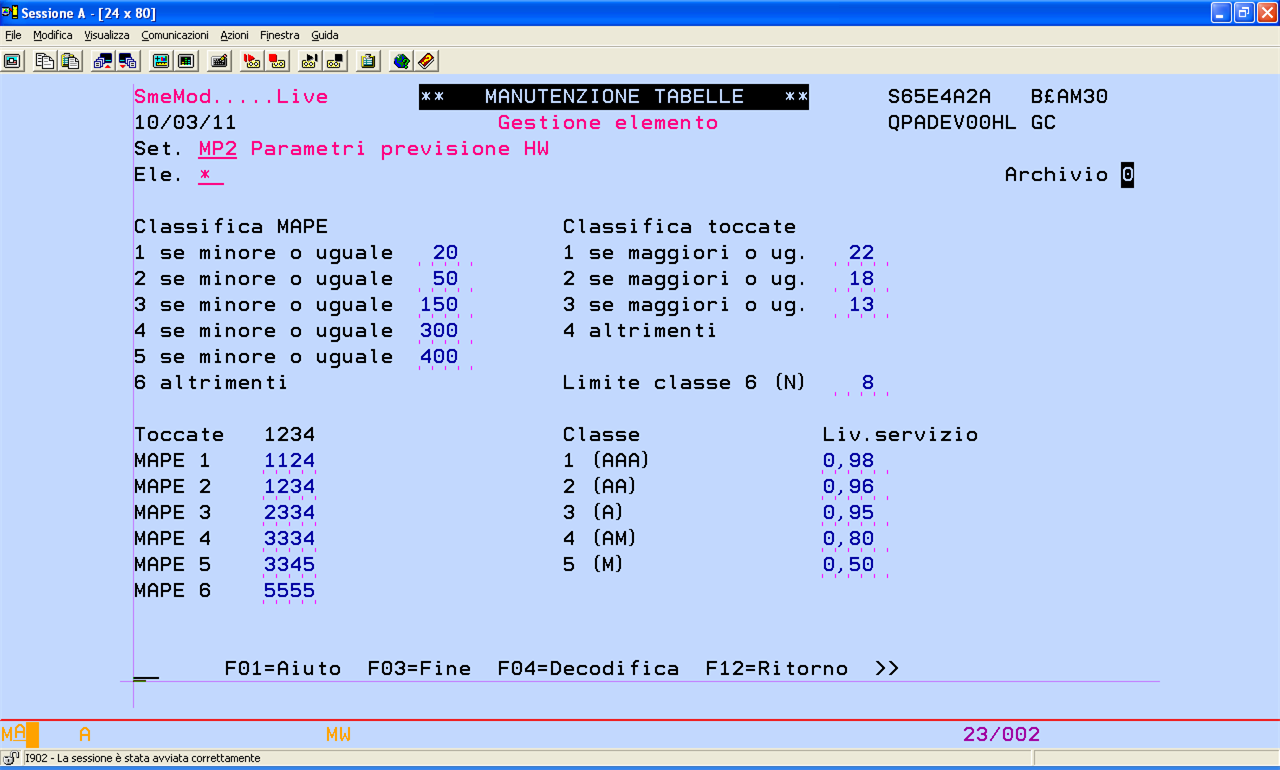 |
Si ricorda che la classe previsiva ottenuta dal calcolo delle previsioni più recente, è ritornata nell'OAV J/H01 dell'articolo (e articolo/plant).
Nella tabella MP2 è inoltre impostabile il livello di servizio che si vuol assicurare per ogni classe previsiva (un valore zero significa che non si vuol calcolare la scorta).
E' possibile inoltre, nell'archivio Articolo/Plant, a livello di articolo, impostare un livello di servizio specifico, memorizzato nel parametro £01 della classe £M. (NB: subsettori ed elementi di tabella di questi parametri sono creati all'ingresso del programma, se inesistenti). A questo punto si è stabilito il livello di servizio dell'articolo, che è ritornato nell'OAV J/H02.
Nell'OAV J/H03 è ritornato, se presente, il livello di servizio specifico dell'articolo.
Per ogni livello di servizio esiste un valore K che, moltiplicato per l'incertezza proporzionale, ritorna il valore della scorta minima.
La tabella di corrispondenza tra livello di servizio e K, è stata inserita all'interno del programma GMGMA_01.
Il legame è, fino ad un livello di servizio dello 0,8, approssimativamente lineare; per questo motivo il passo è stato infittito nella zona tra 0,8 e 1.
Se si imposta un livello di servizio 1, viene assunto un valore di 0,999, a cui corrisponde un K maggiore del 28 % rispetto a quello per un livello di 0,99.
La figura seguente mostra la curva di interpolazione tra livello di servizio e coefficiente K:
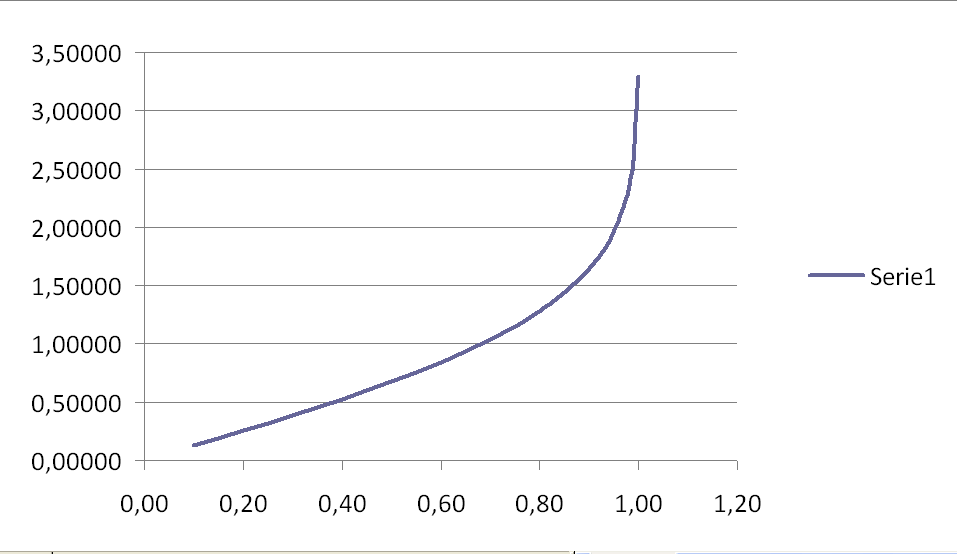 |
Modalità di richiamo - In fonti di disponibilità
Nell'impostazione delle fonti che ritornano la scorta (origine SC, SD) è possibile impostare, tra i parametri di input della fonte, il campo priorità di scelta. Modalità di richiamo - In routine £M5A
Nel richiamo della funzione £M5A (ritorno informazioni articolo/plant) è possibile impostare, tra i parametri di input, il campo priorità di scelta. Fonti esistenti e future
* M5E - SC - Scorta minima* M5F - SD - Scorta datata
Popolamento dati articolo/plant
La scorta dinamica viene calcolata se è stato impostato, nell'archivio articolo/plant, il criterio £01 nel campo "Calcolo scorta lotti". Dato che il comportamento di default non può variare, per attivare questo calcolo è necessario valorizzare il campo con una funzione ad hoc (ad esempio con un UPDATE di SQL). Non è stato realizzato un programma standard di popolamento in quanto le situazioni possono essere le più diversificate: si può voler calcolare la scorta dinamica solo sugli articoli di una determinata classe, oppure ad un determinato livello di risalita, solo per un plant, ecc ... Analisi azione utente MPAP01_X
Il programma di azioni utente MPAP01_X deve esistere, perchè viene richiamato dal programma standard a cui ritorna le eventuali azioni utente, e quindi, se non modificato, resta nella libreria standard. Dato che erroneamente, nel febbraio 2008, sono stati aggiunti gli operatori standard SIV2 e NOV2, si è creato una certa confusione in presenza di azioni utente (programma MPAP01_X in una libreria specifica).Se il programma MPAP01_X è nella libreria personale:
- Se contiene i soli operatori SIV2 e NOV2 lo si cancella (sia come sorgente sia come oggetto) e si lascia il programma nella libreria standard.
- Se contiene altri operatori:
- Lo si rinomina come MPAP01_XO
- Si copia il nuovo MPAP01_X dalla libreria standard in quella di personalizzazione.
- Si copiano gli operatori da MPAP01_XO in MPAP01_X (ad eccezione di SIV2 e NOV2, se presenti).
- Lo si rinomina come MPAP01_XO
Add new attachment
Only authorized users are allowed to upload new attachments.
G’day (anonymous guest)
My Prefs
JSPWiki v2.8.0
